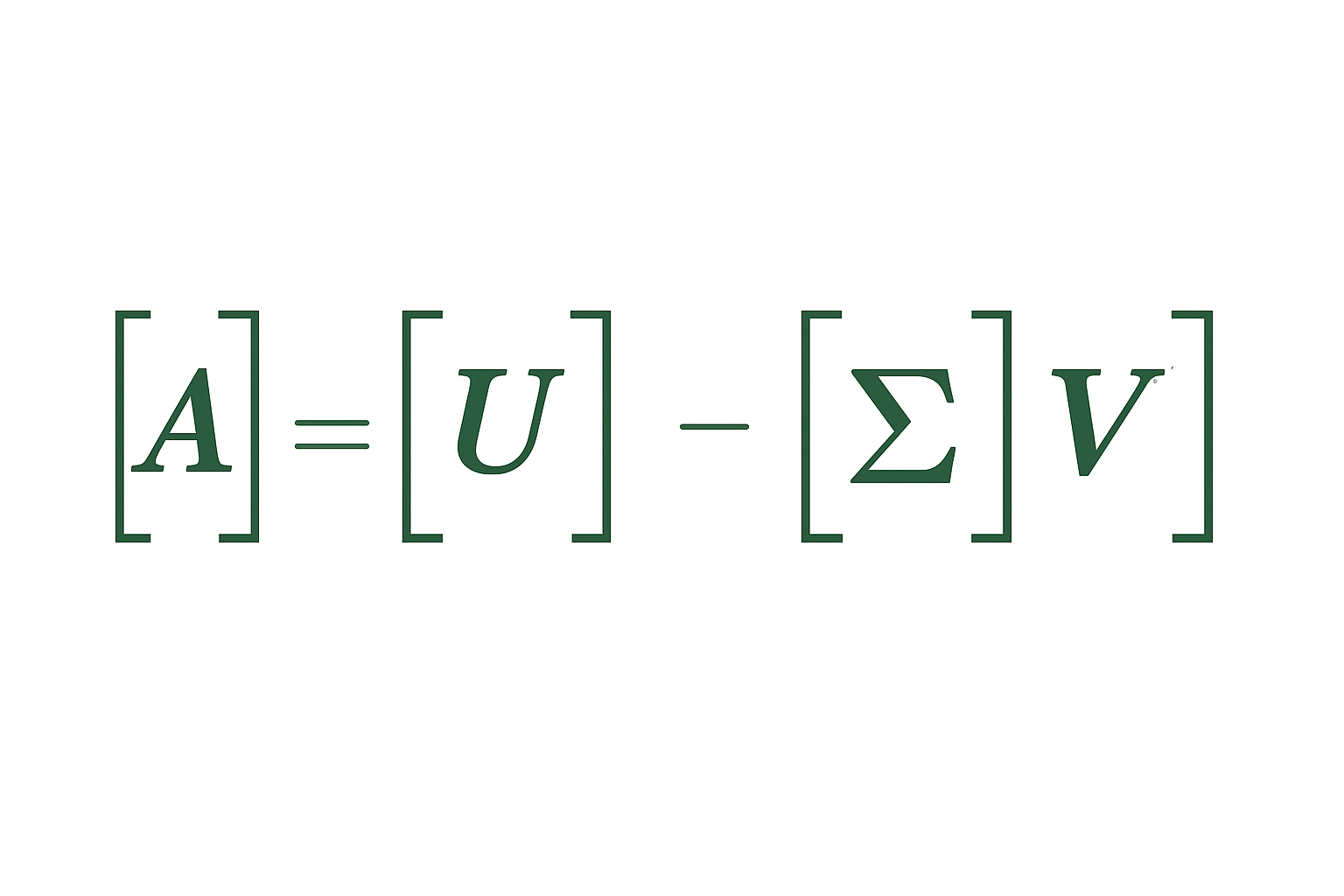SVD factors any matrix into three pieces. Unlike eigendecomposition, works for non-square matrices. The Swiss Army knife of matrix methods.
The decomposition
Any matrix A (m×n) can be written as:
$$A = U\Sigma V^T$$
Where:
- U is m×m orthogonal (columns are left singular vectors)
- Σ is m×n diagonal (singular values on diagonal)
- V is n×n orthogonal (columns are right singular vectors)
Interactive demo: SVD Animation
Computing SVD
import numpy as np
A = np.random.randn(5, 3)
U, s, Vt = np.linalg.svd(A)
# s is 1D array of singular values
# Full reconstruction
S = np.zeros((5, 3))
np.fill_diagonal(S, s)
A_reconstructed = U @ S @ Vt
Or for “economy” SVD (smaller matrices):
U, s, Vt = np.linalg.svd(A, full_matrices=False)
What singular values mean
Singular values are always non-negative, usually sorted largest to smallest.
They measure how much the matrix “stretches” in each direction.
- σ₁: maximum stretch
- σₙ: minimum stretch (or 0 for rank-deficient)
Low-rank approximation
Key property: truncated SVD gives best rank-k approximation.
Keep only top k singular values: $$A_k = U_k\Sigma_k V_k^T$$
This minimizes ||A - A_k|| among all rank-k matrices.
k = 2
A_approx = U[:, :k] @ np.diag(s[:k]) @ Vt[:k, :]
Applications
Image compression:
# Image as matrix
from PIL import Image
img = np.array(Image.open('photo.jpg').convert('L'))
U, s, Vt = np.linalg.svd(img)
# Keep top 50 components
k = 50
compressed = U[:, :k] @ np.diag(s[:k]) @ Vt[:k, :]
Dimensionality reduction (similar to PCA):
# Project data to k dimensions
X_reduced = X @ Vt[:k].T
Recommender systems:
# User-item matrix
# Factor into user features and item features
# Handle missing values with specialized algorithms
SVD vs Eigendecomposition
| Property | SVD | Eigendecomposition |
|---|---|---|
| Matrix shape | Any | Square only |
| Values | Always real, non-negative | Can be complex |
| Vectors | Two sets (U, V) | One set |
| Exists | Always | Not always |
For symmetric A: singular values = |eigenvalues|
Truncated SVD for sparse matrices
Full SVD on huge sparse matrix? Expensive and dense result.
Use randomized/truncated SVD:
from sklearn.decomposition import TruncatedSVD
svd = TruncatedSVD(n_components=100)
X_reduced = svd.fit_transform(X_sparse)
Works directly on sparse matrices. Much faster.
SVD decomposition makes sense? Drop a ⭐ on ML Animations and share this with other ML practitioners!