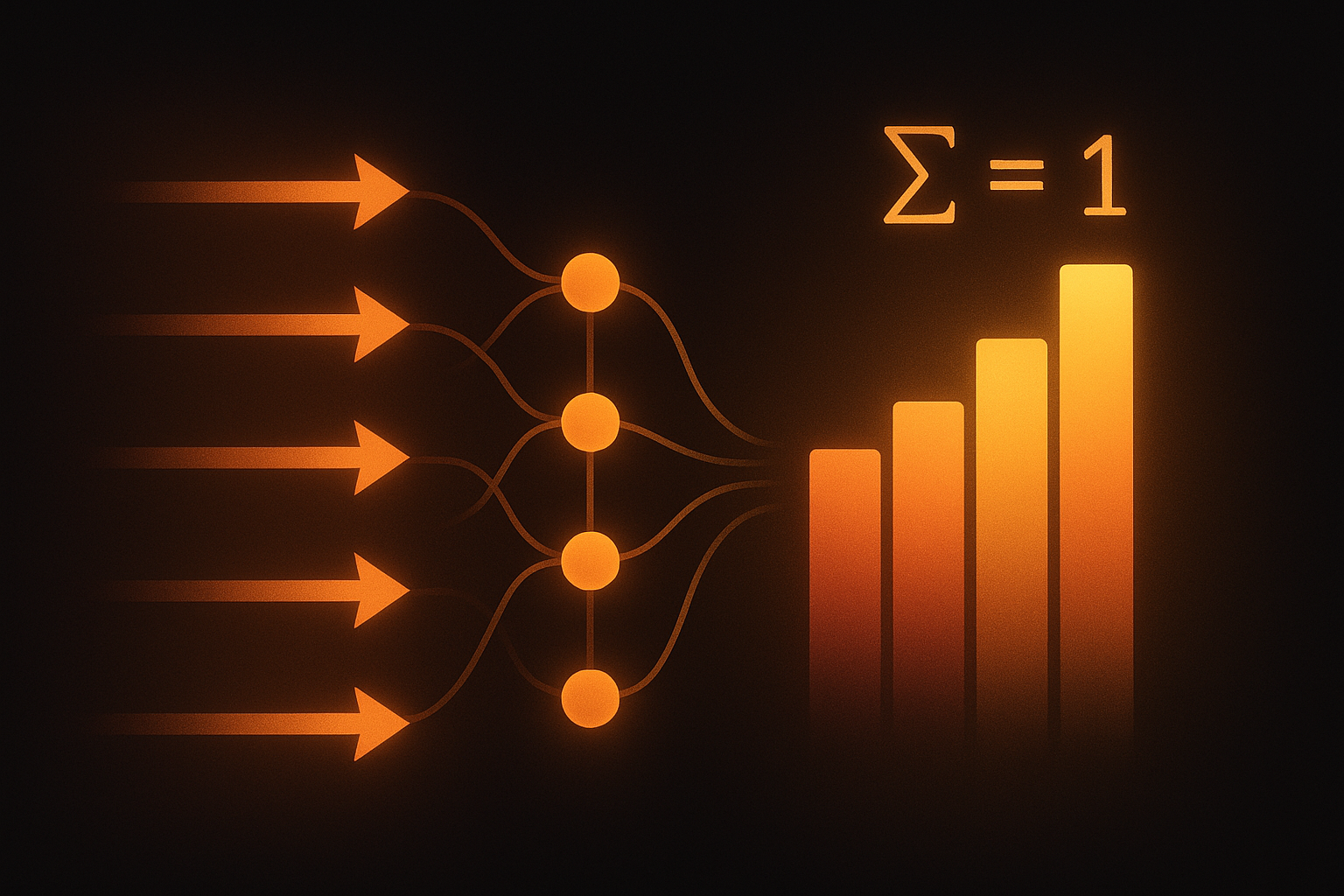
Neural network outputs raw numbers (logits). For classification, you want probabilities. Softmax does that conversion.

The formula

Given vector z of logits:

$$\text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{K} e^{z_j}}$$

Each output becomes probability. All outputs sum to 1.

def softmax(z):
    exp_z = np.exp(z)
    return exp_z / exp_z.sum()

logits = [2.0, 1.0, 0.1]
probs = softmax(logits)  # [0.659, 0.242, 0.099]

Interactive demo: Softmax Animation

What it does

• Positive logit → high probability
• Negative logit → low probability
• Largest logit → highest probability
• Preserves ranking
• Outputs always in [0, 1]
• Sum always 1

Why exponential?

We need positive numbers that preserve relative ordering.

Could use other functions but exp has nice properties:

• Always positive
• Monotonic
• Differentiable everywhere
• Mathematically convenient

Numerical stability

Naive implementation has problems:

logits = [1000, 1001, 1002]
np.exp(logits)  # [inf, inf, inf] - overflow!

Fix: subtract max before exp

def stable_softmax(z):
    z = z - np.max(z)  # shift so max is 0
    exp_z = np.exp(z)
    return exp_z / exp_z.sum()

Now exp never gets input > 0. No overflow.

Most libraries do this automatically.

Temperature

Control how “sharp” the distribution is:

$$\text{softmax}(z_i, T) = \frac{e^{z_i/T}}{\sum_j e^{z_j/T}}$$

T = 1: normal softmax T < 1: sharper, more confident T > 1: softer, more uniform

def softmax_with_temp(z, temperature=1.0):
    z = z / temperature
    return stable_softmax(z)

Used in:

• Knowledge distillation (soft labels)
• Generation (controlling randomness)
• Attention (sometimes)

Softmax vs other activations

Softmax - multiclass classification output Sigmoid - binary classification or multi-label ReLU - hidden layers

Softmax is for output layer when you have mutually exclusive classes.

With cross-entropy loss

Almost always used together:

$$L = -\sum_i y_i \log(\text{softmax}(z_i))$$

Mathematically: $$\frac{\partial L}{\partial z_i} = \text{softmax}(z_i) - y_i$$

Beautiful gradient. Just predicted minus actual.

In code, use combined function:

# PyTorch - these are equivalent but second is more stable
loss1 = nn.CrossEntropyLoss()(logits, targets)
loss2 = nn.NLLLoss()(F.log_softmax(logits), targets)

Log softmax

Often want log of softmax probabilities:

$$\log\text{softmax}(z_i) = z_i - \log\sum_j e^{z_j}$$

More numerically stable than log(softmax(z)).

# Bad - can get log(0) = -inf
log_probs = np.log(softmax(z))

# Good
log_probs = F.log_softmax(z, dim=-1)

Softmax in attention

Attention scores use softmax:

$$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$$

Converts similarity scores to attention weights that sum to 1.

Common confusions

“Softmax regression” = logistic regression for multiclass. The model is linear, softmax just converts to probabilities.

Independent vs mutually exclusive:

• Mutually exclusive classes (cat OR dog) → softmax
• Independent labels (has_cat AND has_dog) → sigmoid per label