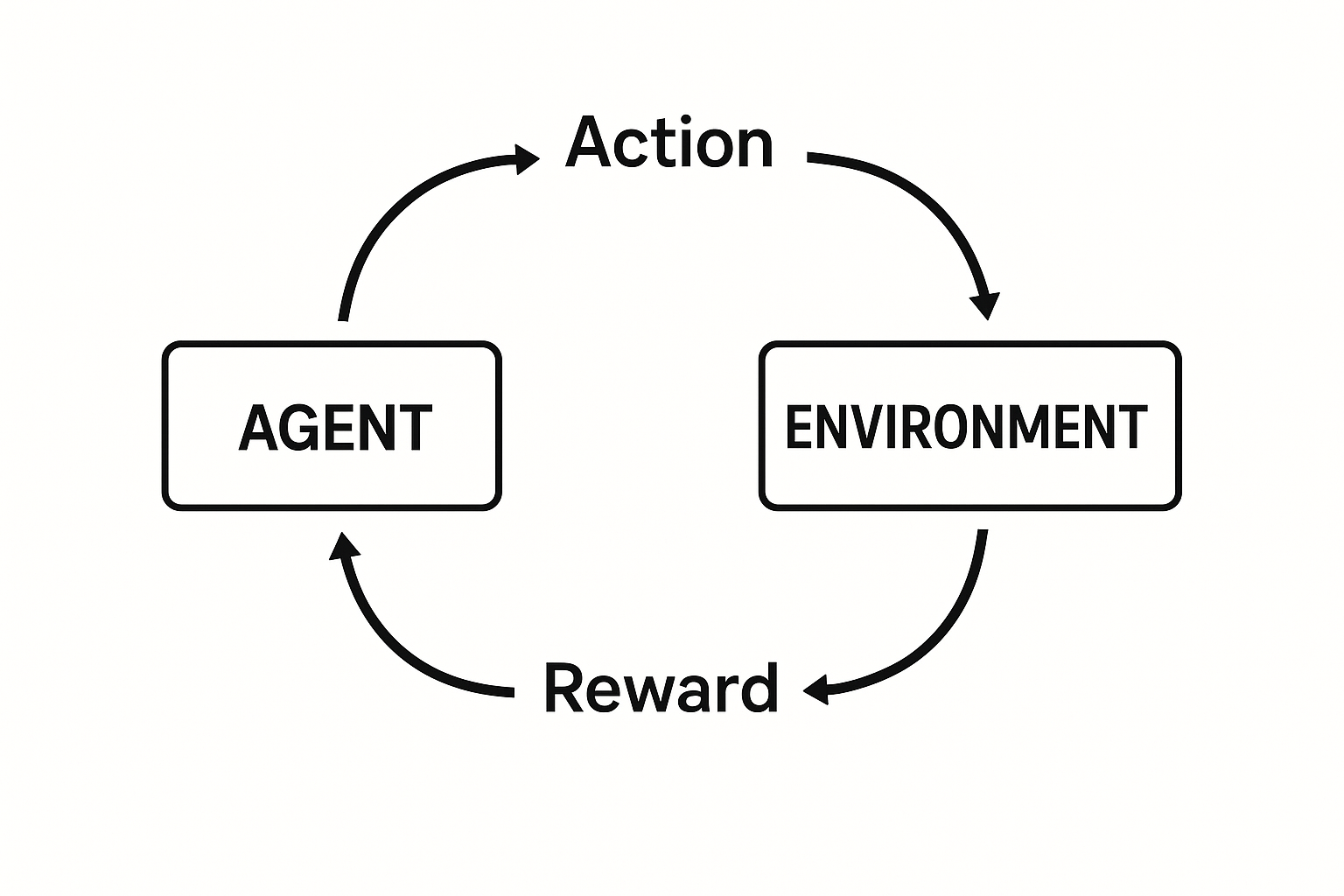
Supervised learning needs labeled data. What if there’s no teacher? RL learns from interaction - take actions, observe outcomes, maximize reward.

How games are mastered. How robots learn to walk.

The setup

Agent: The learner/decision maker Environment: Everything the agent interacts with State (s): Current situation Action (a): What agent can do Reward (r): Feedback signal Policy (π): Strategy - maps states to actions

See the agent-environment loop: RL Foundations Animation

The goal

Find policy π that maximizes expected cumulative reward:

$$G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + … = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}$$

γ (gamma) is discount factor. Future rewards worth less than immediate.

γ = 0: greedy, only care about next reward γ = 1: far-sighted, all rewards equal

Value functions

State value V(s): Expected return starting from state s, following policy π

$$V^\pi(s) = E_\pi[G_t | S_t = s]$$

Action value Q(s,a): Expected return taking action a in state s, then following π

$$Q^\pi(s, a) = E_\pi[G_t | S_t = s, A_t = a]$$

If you know Q*, optimal policy is easy: pick action with highest Q.

Bellman equations

Value functions satisfy recursive relationships:

$$V^\pi(s) = \sum_a \pi(a|s) \sum_{s’,r} p(s’,r|s,a)[r + \gamma V^\pi(s’)]$$

Current value = immediate reward + discounted future value.

For optimal: $$V^(s) = \max_a \sum_{s’,r} p(s’,r|s,a)[r + \gamma V^(s’)]$$

Types of RL

Model-based: Learn environment dynamics, plan ahead Model-free: Learn directly from experience

On-policy: Learn about policy currently executing Off-policy: Learn about different policy than executing

Value-based: Learn value function, derive policy Policy-based: Learn policy directly Actor-critic: Learn both

Simple example: Gridworld

S . . G
. X . .
. . . .

S = start, G = goal (+1), X = pit (-1)

Actions: up, down, left, right

Agent learns: avoid pit, reach goal efficiently.

Code sketch

class Agent:
    def __init__(self, n_states, n_actions):
        self.Q = np.zeros((n_states, n_actions))
    
    def choose_action(self, state, epsilon):
        if np.random.random() < epsilon:
            return np.random.randint(self.n_actions)  # explore
        return np.argmax(self.Q[state])  # exploit
    
    def learn(self, state, action, reward, next_state, done):
        # Q-learning update (see next article)
        target = reward + (0 if done else gamma * np.max(self.Q[next_state]))
        self.Q[state, action] += alpha * (target - self.Q[state, action])

Challenges

Credit assignment: Which actions led to reward received much later? Exploration vs exploitation: Try new things or stick with what works? Sample efficiency: Learning from limited experience Stability: Function approximation can diverge