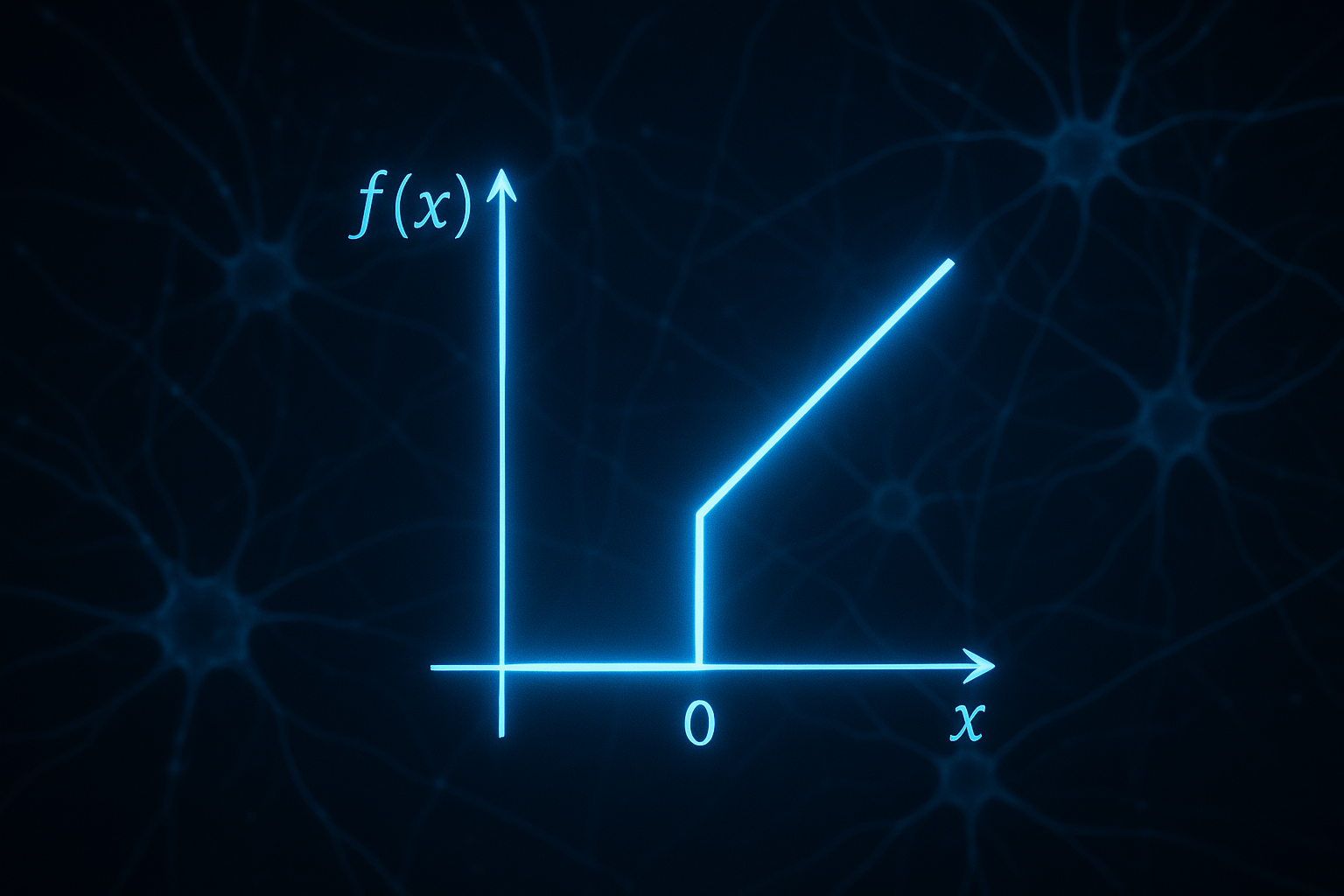Sigmoid was the standard activation function for decades. Then ReLU came along and made deep learning actually work. The crazy part? It’s embarrassingly simple.

What is ReLU?

Rectified Linear Unit. The whole thing is just:

$$f(x) = \max(0, x)$$

• Negative inputs → 0 (just throw them away)
• Positive inputs → pass through unchanged

def relu(x):
    return max(0, x)

# or with numpy
def relu(x):
    return np.maximum(0, x)

That’s literally it. A bent line. And it revolutionized the field.

Interactive demo: ReLU Animation - watch how gradients flow through the network.

Why sigmoid was a problem

Before ReLU, everyone used sigmoid: $\sigma(x) = \frac{1}{1 + e^{-x}}$

Looks smooth and pretty, but it has killer problems:

Problem 1: Vanishing gradients

Sigmoid’s derivative maxes out at 0.25. In a deep network, gradients multiply through layers:

$$0.25 \times 0.25 \times 0.25 \times … = \text{basically zero}$$

After 10 layers, your gradient is 0.0000009. The early layers never learn anything because the learning signal dies before reaching them.

Problem 2: Saturation

For very negative or very positive inputs, sigmoid is almost flat. Gradient ≈ 0. Neurons get “stuck” and stop learning entirely.

Problem 3: Expensive

Computing exponentials is slow. In a network with millions of activations, this adds up.

How ReLU fixes everything

Gradient is 1 for positive inputs

No matter how deep your network, if the input is positive, the gradient passes through at full strength. Signal doesn’t die!

No saturation on the positive side

Big positive values? Still gradient of 1. No getting stuck.

Blazing fast

It’s literally just if x > 0 then x else 0. Your GPU loves this.

The catch: dying neurons

ReLU has one annoying problem. On the negative side, gradient is exactly 0.

If a neuron consistently receives negative inputs, it outputs 0 forever. With gradient 0, it can never recover. It’s “dead.”

This happens when:

• Learning rate is too high (weights swing too far)
• Bad initialization
• Unlucky input distribution

Some networks end up with 20-40% dead neurons. Still works, but wasteful.

Leaky ReLU

Small slope for negative values:

$$f(x) = \begin{cases} x & x > 0 \ 0.01x & x \leq 0 \end{cases}$$

def leaky_relu(x, alpha=0.01):
    return np.where(x > 0, x, alpha * x)

Dead neurons can recover. Still fast.

Other variants

PReLU (Parametric ReLU)

Like Leaky but alpha is learned per channel.

ELU $$f(x) = \begin{cases} x & x > 0 \ \alpha(e^x - 1) & x \leq 0 \end{cases}$$

Smooth, pushes mean activations toward zero.

GELU (Gaussian Error Linear Unit)

$$f(x) = x \cdot \Phi(x)$$

Where Φ is CDF of standard normal. Used in BERT, GPT.

Swish/SiLU $$f(x) = x \cdot \sigma(x)$$

Google found it through automated search. Works well.

Which one to use?

For most cases: ReLU or Leaky ReLU

For transformers: GELU

For very deep networks: Check if dead neurons are a problem, switch to Leaky if so

Don’t overthink it. Difference is usually small.

Code examples

PyTorch:

import torch.nn as nn

# In Sequential
model = nn.Sequential(
    nn.Linear(100, 50),
    nn.ReLU(),
    nn.Linear(50, 10)
)

# Other activations
nn.LeakyReLU(0.01)
nn.ELU()
nn.GELU()

TensorFlow:

import tensorflow as tf

model = tf.keras.Sequential([
    tf.keras.layers.Dense(50, activation='relu'),
    tf.keras.layers.Dense(10)
])

Simple but powerful, right? If you found this useful, star ML Animations and share it on Twitter!