Self-attention is permutation equivariant. Shuffle the input tokens, output shuffles the same way. The model has no idea what’s first or last.

That’s a problem. Word order matters! We need to inject position information.

The issue

Consider: “The dog bit the man” vs “The man bit the dog”

Same tokens, different meaning. Pure attention treats them identically.

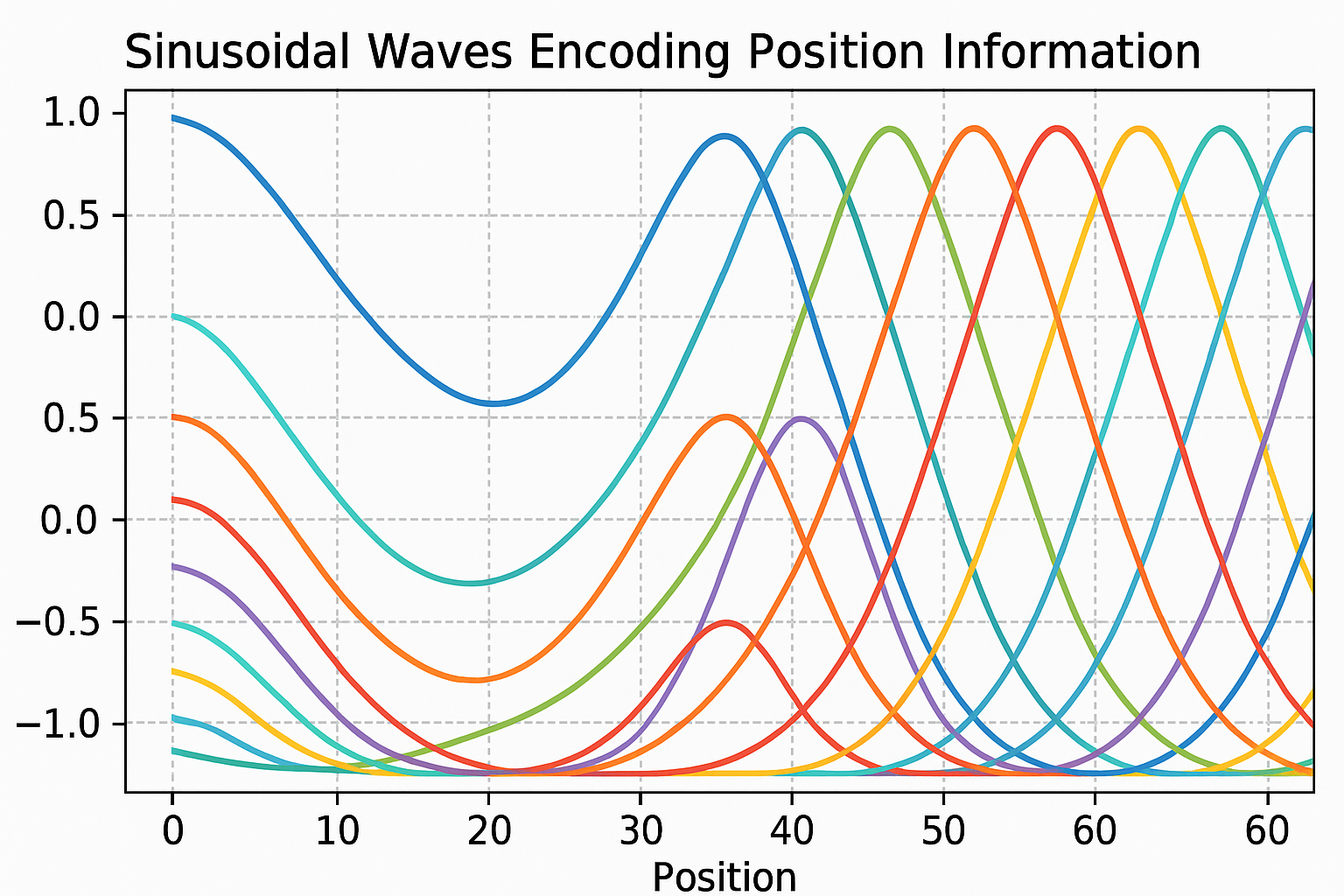
Sinusoidal encoding (original transformer)

Add position vectors to token embeddings. Use sine and cosine of different frequencies:

$$PE_{(pos, 2i)} = \sin(pos / 10000^{2i/d_{model}})$$ $$PE_{(pos, 2i+1)} = \cos(pos / 10000^{2i/d_{model}})$$

Each dimension has a different wavelength. Position 0 has different pattern than position 100.

See the wave patterns: Positional Encoding Animation

Why sinusoids?

1. Bounded: Values between -1 and 1
2. Deterministic: No extra parameters to learn
3. Extrapolation: Works for positions longer than training
4. Relative positions: PE(pos+k) can be expressed as linear function of PE(pos)

Code

def sinusoidal_encoding(max_len, d_model):
    pe = torch.zeros(max_len, d_model)
    position = torch.arange(0, max_len).unsqueeze(1)
    div_term = torch.exp(torch.arange(0, d_model, 2) * (-np.log(10000.0) / d_model))
    
    pe[:, 0::2] = torch.sin(position * div_term)
    pe[:, 1::2] = torch.cos(position * div_term)
    
    return pe  # (max_len, d_model)

# Usage: add to token embeddings
x = token_embeddings + positional_encoding[:seq_len]

Learned positional embeddings

Alternative: learn position embeddings like word embeddings.

pos_embedding = nn.Embedding(max_len, d_model)
positions = torch.arange(seq_len)
x = token_embeddings + pos_embedding(positions)

Works well in practice. Used by BERT, GPT-2.

Downside: can’t extrapolate beyond max_len.

Relative positional encoding

Instead of “position 5”, encode “3 positions apart”.

More natural for many relationships. “Adjective before noun” is relative.

Transformer-XL, T5 use relative position biases added to attention scores.

RoPE (Rotary Position Embedding)

Used by LLaMA, modern models. Elegant idea:

Rotate query and key vectors by angle proportional to position.

def apply_rope(x, positions):
    # x: (..., d)
    # Split into pairs, rotate each pair
    d = x.shape[-1]
    freqs = 1.0 / (10000 ** (torch.arange(0, d, 2) / d))
    angles = positions.unsqueeze(-1) * freqs
    
    cos = torch.cos(angles)
    sin = torch.sin(angles)
    
    x1, x2 = x[..., ::2], x[..., 1::2]
    return torch.stack([x1*cos - x2*sin, x1*sin + x2*cos], dim=-1).flatten(-2)

When you compute q·k, the rotation encodes relative position. Mathematically elegant, works great in practice.

ALiBi (Attention with Linear Biases)

Even simpler. Add bias to attention scores:

$$\text{score}_{ij} = q_i \cdot k_j - m \cdot |i - j|$$

Penalty proportional to distance. Different heads use different slopes m.

No position embedding at all. Just modify attention.