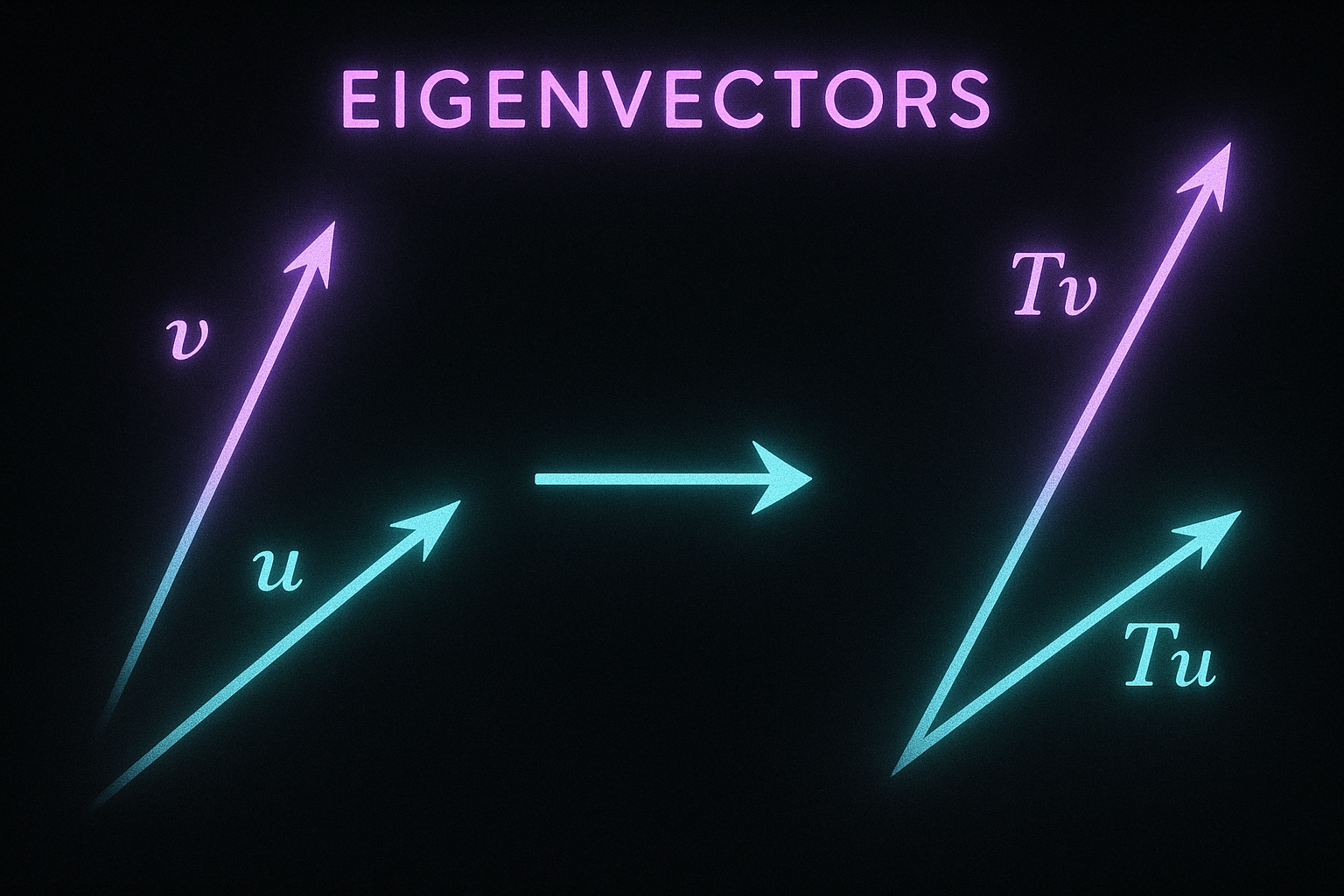
A matrix transforms vectors. Eigenvectors are special directions that only get scaled, not rotated. Eigenvalues tell you the scale factor.

Sounds abstract but used everywhere - PCA, spectral clustering, stability analysis, PageRank.

Definition

For matrix A, eigenvector v and eigenvalue λ satisfy:

$$Av = \lambda v$$

Apply matrix → just multiplies by scalar. Direction unchanged.

See the transformation: Eigenvalue Animation

Finding eigenvalues

Rewrite: Av = λv → (A - λI)v = 0

For non-trivial v, matrix (A - λI) must be singular:

$$\det(A - \lambda I) = 0$$

This gives the characteristic polynomial. Roots are eigenvalues.

For 2×2 matrix:

A = [a  b]
    [c  d]

det(A - λI) = (a-λ)(d-λ) - bc = λ² - (a+d)λ + (ad-bc) = 0

Computing in practice

Don’t solve characteristic polynomial for large matrices. Use numerical methods.

import numpy as np

A = np.array([[4, 2], [1, 3]])

# Eigenvalues and eigenvectors
eigenvalues, eigenvectors = np.linalg.eig(A)

print(eigenvalues)    # [5. 2.]
print(eigenvectors)   # columns are eigenvectors

Properties

Real symmetric matrices:

• All eigenvalues are real
• Eigenvectors are orthogonal
• Can be diagonalized

Trace = sum of eigenvalues: $$\text{tr}(A) = \sum \lambda_i$$

Determinant = product of eigenvalues: $$\det(A) = \prod \lambda_i$$

PCA connection

Principal Component Analysis uses eigenvalues.

1. Compute covariance matrix of data
2. Find eigenvectors (principal components)
3. Eigenvalues tell variance explained

# PCA from scratch
X_centered = X - X.mean(axis=0)
cov = X_centered.T @ X_centered / len(X)
eigenvalues, eigenvectors = np.linalg.eigh(cov)

# Sort by eigenvalue (descending)
idx = np.argsort(eigenvalues)[::-1]
principal_components = eigenvectors[:, idx]

Or just use sklearn:

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X)

Spectral decomposition

If A is symmetric, it can be written as:

$$A = Q\Lambda Q^T$$

Where:

• Q has eigenvectors as columns
• Λ is diagonal matrix of eigenvalues

This is powerful for matrix analysis.

Power iteration

Simple algorithm to find largest eigenvalue:

def power_iteration(A, num_iters=100):
    v = np.random.randn(A.shape[0])
    v = v / np.linalg.norm(v)
    
    for _ in range(num_iters):
        v = A @ v
        v = v / np.linalg.norm(v)
    
    eigenvalue = v @ A @ v
    return eigenvalue, v

Converges to dominant eigenvector. Used in PageRank!

Eigenvalues and stability

For differential equations dx/dt = Ax:

• All eigenvalues negative → stable (decays)
• Any eigenvalue positive → unstable (grows)
• Complex eigenvalues → oscillation

In neural networks, eigenvalues of weight matrices relate to gradient flow.

Condition number

Ratio of largest to smallest eigenvalue (for symmetric positive definite):

$$\kappa(A) = \frac{\lambda_{max}}{\lambda_{min}}$$

Large condition number = ill-conditioned = numerical problems.

cond = np.linalg.cond(A)
# If very large, matrix is nearly singular