A set that uses almost no memory. Trade-off: might say “yes” when answer is “no” (false positive). But never says “no” when answer is “yes” (no false negatives).
Weird but incredibly useful.
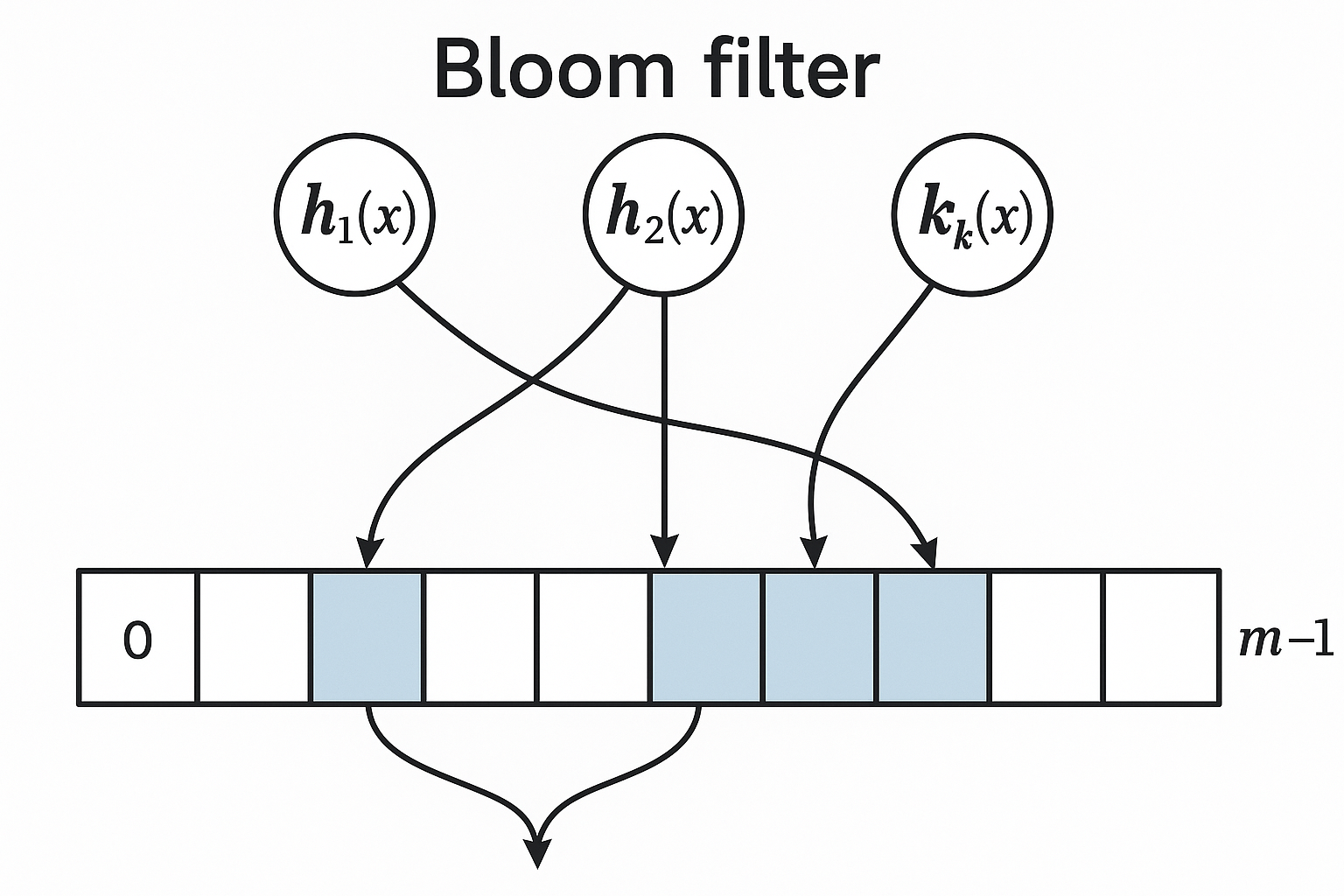
How it works
- Bit array of size m (all zeros initially)
- k different hash functions
Insert: Hash item k times. Set those k bits to 1. Query: Hash item k times. All k bits are 1? Probably in set. Any bit is 0? Definitely not in set.
Interactive demo: Bloom Filter Animation
Why false positives happen
Different items might hash to same positions.
Insert “cat”: sets bits 2, 7, 13 Insert “dog”: sets bits 4, 7, 18
Query “bird”: hashes to 2, 4, 13
All those bits are 1 (from cat and dog). Bloom filter says “probably yes” even though bird was never added.
False positive rate
Probability of false positive:
$$p \approx \left(1 - e^{-kn/m}\right)^k$$
Where:
- n: number of items inserted
- m: number of bits
- k: number of hash functions
Optimal k given m and n: $$k = \frac{m}{n}\ln 2$$
Sizing the filter
For desired false positive rate p with n items:
$$m = -\frac{n \ln p}{(\ln 2)^2}$$
Example: 1 million items, 1% false positive rate → need 9.6 million bits (1.2 MB).
Compare to storing 1 million strings directly!
Implementation
import hashlib
class BloomFilter:
def __init__(self, size, num_hashes):
self.size = size
self.num_hashes = num_hashes
self.bit_array = [0] * size
def _hashes(self, item):
hashes = []
for i in range(self.num_hashes):
h = hashlib.md5(f"{item}{i}".encode()).hexdigest()
hashes.append(int(h, 16) % self.size)
return hashes
def add(self, item):
for pos in self._hashes(item):
self.bit_array[pos] = 1
def might_contain(self, item):
return all(self.bit_array[pos] for pos in self._hashes(item))
Real-world uses
Web browsers: Check if URL might be malicious. False positive = extra check. False negative = security hole.
Databases: Check if key might exist before expensive disk read. Cassandra, HBase, LevelDB all use this.
Spell checkers: Is word probably in dictionary?
Network routers: Has this packet been seen before?
Memory comparison
| Method | Memory for 1M items |
|---|---|
| Hash set of strings | ~50 MB |
| Bloom filter (1% FP) | 1.2 MB |
| Bloom filter (0.1% FP) | 1.8 MB |
Bloom filters are elegant, aren’t they? Star ML Animations and share this with your systems programming friends!